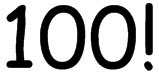
На сколько нулей будет оканчиваться число 100! после перемножения всех сомножителей? Приветствуются ответы с объяснениями.
Как с помощью двух четверок получить 64?
Как с помощью двух четверок получить 64?
update
Первый - 67108864.Ответ
24.
Количество нулей будет равно количеству чисел 10 среди множителей. А так как 10 равно произведению 5 и 2, то искомое число нулей будет равно наименьшему из следующих двух чисел: числа множителей 2 в разложении 100! на простые множители и числа множителей 5 в этом же разложении. Ясно, что двоек будет больше, чем пятёрок. Число 100! содержит 20 чисел кратных 5, среди которых четыре числа кратны 25=5^2 (это 25, 50, 75 и 100). Таким образом, 100! оканчивается на 20+4=24 нулей.
Количество нулей будет равно количеству чисел 10 среди множителей. А так как 10 равно произведению 5 и 2, то искомое число нулей будет равно наименьшему из следующих двух чисел: числа множителей 2 в разложении 100! на простые множители и числа множителей 5 в этом же разложении. Ясно, что двоек будет больше, чем пятёрок. Число 100! содержит 20 чисел кратных 5, среди которых четыре числа кратны 25=5^2 (это 25, 50, 75 и 100). Таким образом, 100! оканчивается на 20+4=24 нулей.
Если говорить про десятичную систему счисления, то
ОтветитьУдалитьочевидно, что [100 / 5] + [100 / 25] = 20 + 4 = 24
Двоек больше пятерок, каждое пятое делится на 5, каждое 25 дает еще степень. На 125 делить уже поздно.
Всё верно!
УдалитьС чего это 100/5 + 100/25 тут что-то очевидно?
УдалитьНу и что. что двоек больше?
Кукую степень даёт 25 и как это связано с задачей?
Если мы 25 * 2 то зачем его второй раз умножать?
Из этого сумбурного объяснения следует, что результат списан с ответа и случайные цифры подогнаны в его оправдание.
у меня 32 нуля получается) если считать по количеству пятерок...
ОтветитьУдалить5, 15, 20, 30, 35, 40... - это по одной пятерке. 25 - это сразу пять пятерок.
25 - встречается 3 раза(25, 50, 100) - это 15 пятерок.
итого 32 пятерки. К ним подбираем по двойке в конце будет 32 нуля)
p.s. оффтоп. А что где когда весенние будут?
Ошибку уже подсказали.
УдалитьНасчёт ЧКГ - первая игра 6 апреля.
Сразу пять пятерок? А с каких пор для факториала берутся слагаемые и затем перемножаются?
ОтветитьУдалитьой)
Удалить