Хорошее продолжение задачи о строительстве моста. Есть два дома: A и B. Между ними протекает река, через которую нужно построить мост. Мост должен быть перпендикулярен берегам реки. Расстояния от домов до ближайших к ним берегов разное. Требуется выбрать для моста такое место, чтобы расстояние от каждого из домов до ближайшего к нему въезда на мост было одинаковым.

update
Первым правильно ответил TheTriomo.Ответ
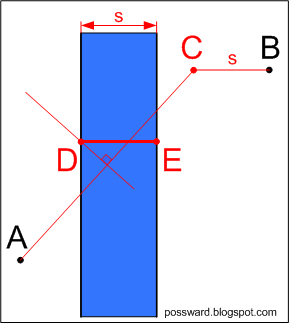
Находим точку C. Далее строим серединный перпендикуляр к AC, который будет пересекать левый берег в точке D. Искомым мостом будет DE. Легко проверить, что AD=BE.

Если я правильно понял задачу, можно решить линейкой и уголком вот так: https://lh3.googleusercontent.com/-S-_Q54HC3Dc/UVVZaJitUMI/AAAAAAAAHrc/xKKJYtALSrI/s0/temp.png
ОтветитьУдалитьМост - красная линия.
УдалитьРасстояния от А до моста: sqrt(a^2 + (b+x)^2)
Расстояние от В до моста: sqrt(b^2 + (a+x)^2)
Разные значения получаются.
Перебрасываем один дом симметрично на другую сторону. Ищем точку пересечения срединного перпендикуляра и берега реки...
ОтветитьУдалитьЗадача может иметь одно, ни одного или дофига решений. Очевидно в каких случаях.
имхо, бесконечно числа решений не будет, т.к. по условию задачи
Удалить> Расстояния от домов до ближайших к ним берегов разное.
Так что ни одного, если дома расположены на прямой, перпендикулярной реке, и одно в других случаях
Да. Согласен.
УдалитьДа, способ подходит.
УдалитьКак-то так вроде получается:
ОтветитьУдалитьПусть мост - CD.
1. Умозрительно "вырезаем" реку, то есть "соединяем" точки С и D - и объединяем их в одну - O. Но где точка O - неизвестно пока, кроме того, что на берегу реки.
2. По построению AC=AO, BD=BO. По условию AC=BD. Значит, AO=BO, то есть надо построить окружность, которая проходит через обе точки A, B, а центр лежит на данной прямой - "реке нулевой ширины".
То есть построение следующее:
1. Строим из точки B перпендикуляр к реке, откладываем ширину реки на нем, получаем точку B'
2. Строим отрезок AB' - это хорда окружности.
3. Строим серединный перпендикуляр к AB'. Центр окружности лежит на нем.
4. Искомая точка O - это точка, в которой перпендикуляр пересекает левый (от нас) берег реки. Она же C. Точка D находится на противоположном берегу реки.
http://smotr.im/dYox
Легко проверить, что отрезки действительно равны - как измерением, так и по построению.
Всё верно. Способ похож на предложенный TheTriomo, только здесь серединный перпендикуляр пересекает другой берег.
Удалитьв ответе на первую задачу
ОтветитьУдалитьпровести серединный перпендикуляр к АС,
точка пересечения с берегом, где точка D, принадлежит мосту