
Имеется 15 одинаковых с виду монет. Одна из них отличается по весу от остальных 14. Тяжелее она или легче - неизвестно. При этом одну из 14 монет с нормальным весом можно легко опознать, так как на ней есть царапина. Как найти монету, которая отличается по весу от остальных, не более чем за три взвешивания на чашечных весах без гирь.
update
Первый - Илья.Ответ
Важно, что монету отличную по весу нужно просто найти, определять её относительный вес не требуется. В схеме взвешиваний, показанной на рисунке, невозможно указать вес монеты с номером 15. Монета с царапиной идёт под номером 10.
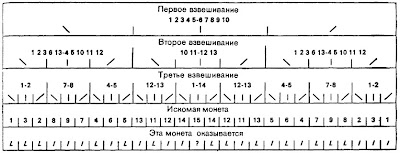
Всего имеем 28 вариантов, значит, полностью задачу разрешить не получится. Это значит, что в каком-то варианте мы не сможем распознать относительный вес фальшивой монеты. Но найти ее тем не менее можно.
ОтветитьУдалитьЗанумеруем монеты так, чтобы эталонная поцарапанная имела номер 15.
Взвешивание номер 1: 1,2,3,4,5 против 6,7,8,9,15.
Случай первый: весы в равновесии.
Взвешивание 2. 10, 11 против 12, 15.
Случай 1.1: весы в равновесии.
Тогда фальшивая - одна из 13, 14. Последним взвешиванием
13 против 15 определим, какая из них фальшивая. Если 14ая - мы так и не узнаем, тяжелая она или легкая.
Остальные случаи довольно классические.
Случай 1.2: 10+11 тяжелее 12+15.
Последним взвешиванием сравниваем 10 и 11. Если одна тяжелее - она и есть фальшивая. Если одинаковые - то фальшивая 12ая, и она более легкая.
Случай 1.3, когда 10+11 легче 12+15, рассматривается аналогично.
Случай второй:1+2+3+4+5 тяжелее 6+7+8+9+15
Второе взвешивание, например, такое:
1,2,8 против 3,4,9.
Случай 2.1. Равновесие.
Тогда третьим взвешиванием сравниваем 6 и 7. Если равны - то фальшивая 5ая, более тяжелая, иначе фальшивая более легкая из 6 и 7.
Случай 2.2. 1+2+8 тяжелее 3+4+9.
Сравниваем 1 и 2. Более тяжелая и будет фальшивой. Если же равны, то фальшивая 9ая - более легкая.
Случай 2.3, когда 1+2+8 легче 3+4+9 рассматривается аналогично.
Последний случай, когда первые пять монет легче - рассматривается аналогично второму.
Этот комментарий был удален автором.
УдалитьСорри, не увидел точки, написал неправильный комментарий.
УдалитьВаше решение абсолютно верное.
Всё верно. В одном из случаев так и не узнаем тяжелее фальшивая монета или легче обычной, но это в задаче и не требуется.
УдалитьНичего не "верно"! Вариантов изначально 14: "одна из 14 монет - фальшивая". Но из-за неопределённости "легче она или тяжелее" весы дают вам не три ответа - "справа, слева или не на весах", а только два: "равно - не равно", и за три взвешивания монету вы найдёте, только если вам очень повезёт...)) Первое взвешивание "по пять, с участием эталонной" - хорошо, если "оправдает" 9 монет на весах, оставив 5 на столе под подозрением, а если наоборот?.. И т.д. Головоломка становится решаемой "за три взвешивания" и действительно поучительной, если вы заведомо знаете, что фальшивка именно "тяжелее остальных", например, "не золотая, а свинцовая с позолотой", или точно знаете, что она "легче остальных" - тогда да: выясняете "пятёрку подозрительных", затем - "пару", и третьим взвешиванием находите монету...
ОтветитьУдалитьУкажите под каким номером должна быть фальшивая монета и какой должен быть её вес относительно нормальной, чтобы её нельзя было обнаружить данным алгоритмом. Так будет понятнее.
Удалить