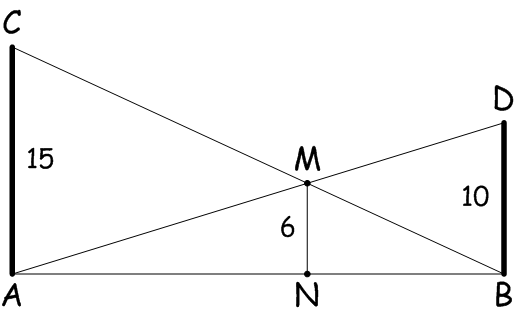
Два столба стоят вертикально на ровной поверхности на некотором расстоянии друг от друга как показано на рисунке. Высота одного столба равна 15 м, высота другого - 10 м. Чему равно расстояние AB между столбами, если известно, что высота точки M над поверхностью равна 6 м?
update
Первым правильно ответил Дмитрий.Ответ
Ещё немного геометрии - чему равна высота треугольника?
Допустим MN на неизвестен.
ОтветитьУдалитьПопробуем его найти.
Из подобия треугольников ABC и NBM следует MN/15=NB/AB.
Из подобия треугольников BAD и NAM следует MN/10=NA/AB.
Складывая левые и правые части получаем MN/15+MN/10=(NB+NA)/AB.
(10MN+15MN)/150=1. MN=6.
Таким образом MN=6 при любом значении AB.
Совершенно верно. Расстояние может быть любым.
Удалить