Проведенные на рисунке диагонали двух внутренних прямоугольников параллельны друг другу. Какая из закрашенных площадей больше: чёрная или оранжевая?

update
Первым был Дмитрий.Ответ
Площади равны.
Один из вариантов решения показан на рисунке. Так как диагонали параллельны, то при их зеркальном отражении они образуют диагональ большого прямоугольника. Площади 1=1', 2=2', а сумма 1+2+3 равна сумме 1'+2'+3'. Следовательно, площадь 3 равна площади 3'.
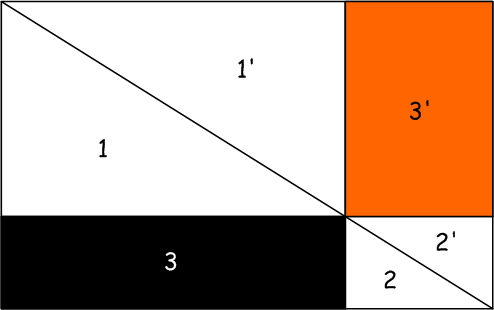
Один из вариантов решения показан на рисунке. Так как диагонали параллельны, то при их зеркальном отражении они образуют диагональ большого прямоугольника. Площади 1=1', 2=2', а сумма 1+2+3 равна сумме 1'+2'+3'. Следовательно, площадь 3 равна площади 3'.

Ещё одна задача из этой серии.
Площади равны (подобие треугольников).
ОтветитьУдалитьЕсть такой вариант. А если не пользоваться подобием?
УдалитьМожно еще и тангенсы посчитать. Впрочем, это все равно подобие треугольников, только другими словами.
ОтветитьУдалитьНо нагляднее всего провести еще две диагонали в тех же прямоугольниках. Из общей симметрии они тоже должны быть параллельны - а по построению и вовсе быть отрезками на большой диагонали. Дальше очевидно.
Да, с диагональю большого прямоугольника получается наглядно.
УдалитьКак раз принадлежность их одной главной диагонали и нужно доказать. Вы этого не сделали.
УдалитьВ прочем, проведя их, мы знаем, что тангенсы у них равны (опираясь на не озвученное нами прямоугольное положение фигуры на бумаге), и есть общая точка -- значит, это один цельный отрезок.
УдалитьА домножив координату Y до превращения фигуры в квадрат, мы не теряем ни параллельность, ни искомое отношение площадей. Но прямоугольники по обе стороны диагонали станут равными.
Могу и полностью. И без тангенсов: иначе это читерство.
УдалитьЛемма.
Дано: два произвольных прямоугольника.
Доказать: если их две диагонали параллельны друг другу, то параллельны друг другу и две другие.
Доказательство: рассмотрим зеркальное отражение прямоугольников с проведенными диагоналями. Видно, что диагонали отобразились в другие диагонали. Следовательно, они также параллельны друг другу (но не первым двум, конечно).
Теперь возвращаемся к рисунку данной задачи.
Левую верхнюю точку на рисунке обозначим A, правую нижнюю - С, а точку, где сходятся цветные прямоугольники - B.
Из Леммы и условия следует, что AB||BC. Следовательно, треугольник ABC - вырожденный. Следовательно, точка B лежит на прямой AC.
А другими словами, диагональ большого прямоугольника проходит через точку "перекрестка".
Ч.Т.Д.
В общем-то и без доказательств понятно, что два параллельных отрезка при зеркальном отражении остаются параллельными, а с общем точкой становятся одним отрезком.
Удалить