Головоломный марафон. Задание 3

Третье задание будет о турнире. В турнире участвовало 8 человек, играли каждый с каждым по одному разу. За победу участник получал 1 очко, за ничью 0.5, а за поражение 0. В результате все участники набрали разное количество очков. Также известно, что второй участник набрал очков столько же, сколько набрали все игроки, занявшие места с 5 по 8. Как сыграли между собой участники, занявшие 4 и 5 места? Ответ обосновать.

Головоломный марафон. Задание 2

Второе задание представляет из себя оригинальную головоломку со спичками: равенство изображенное на рисунке неверно, переложите одну спичку так, чтобы оно выполнялось с точностью до 0.01.

Головоломный марафон. Задание 1

Попробуем сделать решение головоломок еще интереснее. Объявляется КОНКУРС, победитель которого получит приз.
Правила предельно просты. Публикуется задание. Первый, кто напишет в комментариях правильный ответ на вопрос задания, тот получает 1 балл. Один участник может дать только один ответ. Конкурс заканчивается как только один из участников наберет 5 баллов. Победитель получает 500 руб. Сумма небольшая, но и задания не очень сложные.
Для того, чтобы оставить комментарий вам нужно будет зарегистрироваться или воспользоваться уже имеющимся аккаунтом, например, в google. Вознаграждение будет переведено на счет победителя с помощью одной из платежных систем.

Итак, задание №1.
Последнее время увлекся шахматами. Так, что сам придумал задачку. Нужно поставить мат черным в два хода.


Посетителей у блога немного, поэтому шансы на выигрыш велики. Удачи!

UPDATE: Конкурс завершен. Победитель - atrabarba.

Особенные числа

Вот одна нелегкая математическая головоломка. Оказывается, что между числами 53, 317, 599, 797, 3797, 73331, 739397, 2399333, 37337999 много общего. Первое, что приходит на ум, - они все нечетные. Ну, это не очень интересно. Если подумать еще, то можно заметить, что они все простые (то есть делятся без остатка только на 1 и сами на себя). Уже лучше. Но есть еще одна замечательная особенность у этих чисел, которая сразу незаметна. Так что же особенное скрыто в этих числах?
Ответ
Числа эти обладают тем свойством, что после отбрасывания нескольких последних знаков они опять остаются простыми.

Дома и деревья

Это моя интерпретация одной из головоломок Генри Э. Дьюдени. Четыре дачника решили поделить общий участок земли на четыре части. Но на этом участке росло четыре дерева. Каждый из дачников захотел, чтобы у него на участке непременно было дерево. И вот здесь возникла головоломка: как поделить общий участок на четыре части одинаковой площади и формы так, чтобы на каждом из четырех участков были один дом и одно дерево (границы раздела должны проходить по сторонам квадратов, нарисованных на картинке)?
Ответ

Шахматы - 2

Представленная задача в 1842-1844 годах красовалась на обложке одного шахматного журнала. Задание: белые начинают и делают мат в 3 хода.
Ответ
1. Ферзь f5+, король : f5.
2. Конь c: d7, любой возможный ход.
3. Пешка g4, мат.

Шахматы - 1

Несложная шахматная головоломка для разминки. Белая ладья и два коня должны поставить мат черному королю в два хода.
Ответ
1. Ладья белых на f7+, черным остается только конь : f7.
2. Конь на g6, мат.

Головоломные весы

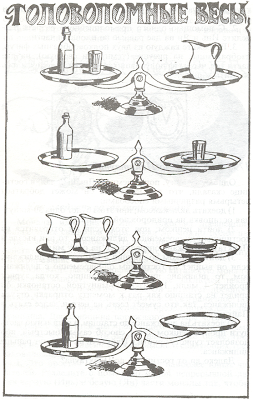Еще одна головоломка от Сэма Лойда в виде картинки. Сколько стаканов уравновесят бутылку?
P.S. На весах, где два кувшина - с другой стороны 3 тарелки.
Ответ
Два кувшина уравновешиваются тремя блюдцами, так что вес одного блюдца равен 2/3 веса кувшина. Теперь добавим на каждую чашу весов второго рисунка по стакану; при этом в левой чаше окажутся те же предметы, что и в левой чаше первого рисунка. Это означает, что вес кувшина равен весу блюдца и двух стаканов; а поскольку вес блюдца равен 2/3 веса кувшина, то вес двух стаканов равен оставшейся 1/3. Следовательно, вес каждого из стакана равен 1/6 веса кувшина.
На первом рисунке мы видим, что стакан (1/6 веса кувшина) и бутылка уравновешивают кувшин; отсюда мы находим, что вес бутылки составляет 5/6 веса кувшина. Таким образом, чтобы уравновесить бутылку на последнем рисунке, требуется 5 стаканов.

Каков возраст жильцов дома?

Когда мне на глаза попалась эта задача, она мне не очень понравилась. Слишком длинное и местами не очень понятное условие. Но все же я решил не сдаваться и попробовать разобраться. В результате потратив часа два получил ответ. Итак, журнал "Квант" за 1970 год предлагает такую задачу.

Агент по переписи Смит и агент по опросу населения Джонс одновременно подходят к дому № 900. Каждый хочет узнать возраст жильцов этого дома. Владелец дома (дело происходит в США) сообщает им свой возраст и говорит, что в доме живут еще три жильца, возрасты которых - три различных целых числа - при перемножении дают число, равное номеру дома. Владелец дома говорит, что он сообщит агенту по переписи возраст среднего из жильцов. Он шепотом сообщает этот возраст агенту по переписи, который после этого говорит, что он не в состоянии определить возраст двух других жильцов. Тогда владелец дома говорит, что он сообщает агенту по опросу сумму возрастов старшего из жильцов и одного из двух других. Он шепотом сообщает сумму агенту по опросу, который говорит, что он тоже не в состоянии отгадать возраст жильцов.
Владелец дома начинает спрашивать их по очереди. В первый раз агент по переписи отвечает, что он не может определить эти возрасты. Агент по опросу говорит, что он тоже не может определить эти возрасты. Во второй раз агент по переписи говорит, что он по-прежнему не может определить возрасты. Агент по опросу говорит, что и он все еще не может этого сделать. В третий раз агент по переписи говорит, что он все еще не знает возрасты жильцов, а агент по опросу заявляет: "Теперь я знаю все возрасты".
Каков возраст этих трех жильцов? (В условии задачи содержится вся необходимая информация для решения!)
Ответ
Полное решение очень громоздкое, поэтому приведу только алгоритм.
Так как возрасты – это целые числа и произведение их равно 900, то вначале раскладываем 900 на 3 целых множителя всеми возможными способами. Получается около 35 вариантов.
Убираем те варианты, в которых присутствует два одинаковых множителя, так как по условия возрасты различны.
Владелец дома сообщил агенту по переписи возраст среднего из жильцов, а агент не смог назвать возрасты остальных. Следовательно, из списка вариантов можно исключить те записи, в которых возраст среднего из жильцов встречается только один раз. Например, вариант 1,25,36. Значение 25 встречается только в этом варианте.
Далее владелец дома сообщает агенту по опросу сумму возрастов старшего и одного из двух других, но агент опять не может назвать возрасты. Это означает, что из списка можно вычеркнуть варианты, в которых сумма возрастов старшего и одного из двух других жильцов встречается только один раз. Например, суммы 52 и 59 подходят только для варианта 2, 9, 50. И если бы возрасты были 2, 9, 50, то агент по опросу мог бы их назвать.
Аналогично следующие три раза, когда владелец дома спрашивает агентов по очереди, вычеркиваем те варианты, которые встречаются только один раз.
В итоге, когда владелец третий раз спрашивает агента по опросу, должны остаться только два варианта: 4, 9, 25 и 5, 9, 20. Так как агент смог назвать возрасты жильцов, то ответом будет вариант 5, 9, 20. Это следует из того, что сумма 34 для варианта 4, 9, 25 отпала на одном из предыдущих этапов, а сумма 29 подходит и для варианта 5, 9, 20. А вот сумма 25 для варианта 5, 9, 20 подходит только для него. Поэтому агенту была названа сумма 25, а ответом будут возрасты 5, 9 и 20.

Задача о пауке и мухе

Наиболее известная головоломка Г. Дьюдени - английского изобретателя головоломок - задача о пауке и мухе. Впервые она была опубликована в 1903 году в одной английской газете.

Комната имеет форму прямоугольного параллелепипеда, размеры которого указаны на рисунке. Посредине боковой стены на расстоянии одного фута от потолка сидит паук. Посредине противоположной стены на высоте одного фута от пола сидит муха. От страха у нее отнялись ноги, и она не может двинуться с места. Спрашивается, каково кратчайшее расстояние, которое должен преодолеть паук для того, чтобы схватить муху?
Ответ
Для решения задачи нужно построить развертку граней прямоугольного параллелепипеда и провести на ней прямую от местонахождения паука к точке, в которой сидит муха. Поскольку построить развертку можно многими способами, то нужно выбрать среди них ту, которая дает кратчайшее расстояние. Ответ показан на рисунке, длина кратчайшего пути от паука к мухе равна 40 футам.

Как поделить деньги?

Два путника сели обедать. У одного было 5 лепешек, а у другого 3. Все лепешки одинаковой стоимости. Подошел к ним третий путник, не имевший чего есть, и предложил пообедать этими лепешками сообща, обещая уплатить им деньгами за ту часть лепешек, которая придется на его долю. Пообедав, он отдал обоим, имевшим лепешки, 8 копеек. Спрашивается: как те два путника должны разделить эти деньги?
Ответ
По условию задачи выходит, что все лепешки стоили 24 коп., так как расход каждого путника равен 8 коп. Отсюда следует, что каждая лепешка стоит 3 коп. Итак, тот путник который дал 5 лепешек, издержал 15 коп., и если вычесть отсюда 8 коп. за лепешки, съеденные им самим, то выходит, что ему нужно из денег третьего путника получить 7 коп. Рассуждая точно так же, находим, что второй путник имел лепешек на 9 коп., и что ему приходится из денег третьего путника получить 1 коп.

Взаимосвязь вещей

Порой довольно своеобразно проявляется взаимосвязь некоторых вещей. Следующие примеры это хорошо демонстрируют. Это две чисто физические задачи школьного уровня, но необычность их формулировок сначала может поставить в тупик.

Первая задача. Даны: кусок нити, металлическая гайка и секундомер. Требуется определить длину нити.
Вторая задача. Даны: стол, небольшой деревянный брусок и транспортир. Требуется определить коэффициент трения между столом и бруском.

Вот такие забавные "бытовые" формулировки. Если же написать текст формализовано, как это делается в учебниках, то станет совсем неинтересно.
Ответ
Для решения первой задачи нужно привязать гайку к нити, у нас получится маятник. Затем с помощью секундомера нужно вычислить период этого маятника. Длина маятника, его период и ускорение свободного падения связаны между собой следующей формулой, откуда находим длину:
Для решения второй задачи кладем брусок на стол. Далее нужно наклонять стол до момента, когда брусок начнет скользит по столу. Транспортиром измеряем угол наклона стола и с помощью следующих формул находим коэффициент трения:

Фальшивые монеты

Существует много вариантов задач со взвешиванием. Один из них предлагает Мартин Гарднер в своей книге "Математические головоломки и развлечения".

Имеется 10 кучек монет, в каждой кучке по 10 монет. Одна кучка целиком состоит из фальшивых монет, но какая именно - неизвестно. Известен лишь вес настоящей монеты, и, кроме того, установлено, что каждая фальшивая монета на один грамм тяжелее, чем нужно. Монеты можно взвешивать на пружинных весах (то есть можно определить вес взвешиваемых монет). Какое минимальное число взвешиваний необходимо произвести, чтобы отыскать кучку, целиком состоящую из фальшивых монет? И каким образом нужно производить взвешивание?
Ответ
Кучку фальшивых монет можно найти с помощью одного-единственного взвешивания. Нужно взять одну монету из первой кучки, две из второй, три – из третьей и т.д. и, наконец, все 10 монет из десятой кучки. Затем все отобранные монеты взвешиваются все вместе на пружинных весах. Лишний вес, выраженный в граммах, будет соответствовать номеру фальшивой кучки.

Перетягивание каната

Задача от мастера головоломок Сэма Лойда. Все условия указаны на рисунке. Кто же перетянет канат в третьем случае?
Ответ
Объединенная «тяга» четырех тучных парней в точности равна тяги пяти пышных сестер. Поскольку на втором рисунке показано, что пара тощих близнецов равна по силе одному тучному парню и двум пышным девицам, мы можем упростить задачу, заменив на третьем рисунке двух тощих близнецов их «тяговым эквивалентом», то есть поставив вместо них толстого парня и двух пышных девиц.
Теперь у нас пять пышных сестер и один тучный парень противостоят одно пышной сестре и четырем тучным парням. Мы может удалить четырех тучных парней с одной и пять пышных девиц с другой стороны каната, ибо, согласно первому рисунку, их силы равны. При этом слева останется один тучный парень, а справа – одна пышная девица. Таким образом, выиграет левая команда, поскольку ее тяговая сила на 1/5 силы парня больше, чем у правой команды.

Задача о двух лодках

Книги Я. И. Перельмана "Занимательная механика", "Занимательная геометрия" и "Занимательная математика" являются теми книгами, которые могут по-настоящему увлечь человека наукой. Советую. Вот несложная задача из "Занимательной механики".

К пристани на озере приближаются две одинаковые лодки. Оба лодочника подтягиваются с помощью веревки. Противоположный конец веревки первой лодки привязан к тумбе на пристани; противоположный же конец веревки второй лодки находится в руках матроса на пристани, который также тянет веревку к себе. Все трое прилагают одинаковые усилия. Какая лодка причалит раньше?
Ответ
На первый взгляд может показаться, что причалит раньше та лодка, которую тянут двое: двойная сила порождает большую скорость. Но верно ли, что на эту лодку действует двойная сила? Если и лодочник и матрос оба тянут к себе веревку, то натяжение веревки равно силе только одного из них – иначе говоря, оно такое же, как и для первой лодки. Обе лодки подтягиваются с равной силой и причалят одновременно.

Лампа для лунной поверхности

Если вы знакомы с теорией решения изобретательских задач (ТРИЗ) и знаете основы физики, то без труда решите следующую изобретательскую задачу.

В книге М. Борисова "Кратеры Бабакина" есть эпизод, связанный с проектированием станции "Луна-16". Нужно было снабдить станцию компактной и сильной электролампой для освещения лунной поверхности "под ногами" станции. Лампе предстояло выдержать большие механические перегрузки. Естественно, отобранные образцы придирчиво испытывали. И вот оказалось, что лампы не выдерживают перегрузок. Слабым местом было соединение цоколя лампы со стеклянным баллоном. Сотрудники Бабакина сбились с ног, пытаясь найти более прочные лампы. Как вы думаете, что предложил в этой ситуации главный конструктор Георгий Николаевич Бабакин?
Ответ
В соответствии с положением об идеальном конечном результате: идеальный баллон - когда баллона нет, а функция его выполняется. В чем функция баллона? Держать вакуум внутри лампы. Но зачем везти вакуум на Луну, если там сколько угодно своего?! Бабакин предложил поставить на "Луну-16" лампу без стеклянного баллона. Такая лампа непригодна на Земле, но ведь на Земле она и не нужна.

Минутная и часовая стрелки часов

В поисках новых головоломок вспомнил о существовании такого замечательного журнала как "Квант". Помню, как ещё в школьные годы мне попался один из номеров и как много времени я потратил на решение напечатанных там задач. Задачи в "Кванте" очень трудные, для решения многих из них помимо сообразительности требуются нетривиальные знания математического аппарата. Но есть задачи, которые можно решить и без сложных вычислений. Хотя от этого они не становятся простыми. Вот одна из них.

Перед вами часы. Сколько существует положений стрелок, по которым нельзя определить время, если не знать, какая стрелка часовая, а какая - минутная? (Считается, что положение каждой из стрелок можно определить точно, но следить за тем, как стрелки двигаются, нельзя)

На рисунке приведен пример одного из таких положений стрелок.
Ответ
Предположим, что рядом с нашими часами (справа) другие, воображаемые, которые идут ровно в 12 раз быстрее. Пустим и те и другие часы одновременно, когда они показывают 12 часов; тогда часовая стрелка правых часов все время совпадает с минутной левых. Ясно, что интересующие нас «неразличимые» положения стрелок – в точности те, когда часовая стрелка левых совпадает с минутной правых, быстрых часов. Сколько же раз это произойдет? Из 12*12=144 оборотов, которые сделает минутная стрелка правых часов за то время, пока часовая стрелка «нормальных» сделает один оборот, на каждом обороте произойдет одно совпадение (включая начальную точку первого оборота); из них нужно исключить 12 случаев, когда совпадают все четыре стрелки, - остается 132. Ответ: существует 132 положения стрелок, удовлетворяющих условиям задачи.

Какую стратегию выбрать?

Про эту задачу мне рассказал приятель из университета. Ему предложили ее решить на собеседовании, когда он устраивался на работу.

Дано прямоугольное поле и круглые фишки. В игре участвуют двое. Игроки по очереди должны класть фишки на любое свободное место поля. Выигрывает тот игрок, чья фишка займет последнее свободное место. Вопрос: какую стратегию должен выбрать игрок, который ходит первым, чтобы точно выиграть?
Ответ
Первую фишку первый игрок должен положить в центр прямоугольника. Каждую следующую фишку он должен класть симметрично фишке второго игрока относительно центра. Таким образом, куда бы не положил фишку второй игрок, на симметричном относительно центра месте всегда будет свободное поле.

Задача от А.П. Чехова

Следующая задача из рассказа Антона Павловича Чехова "Репетитор". Вот отрывок из произведения:

Теперь по арифметике... Берите доску. Какая следующая задача? Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует: - "Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?" Повторите задачу. Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138. - Для чего же это вы делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю! Зиберов делит, получает 3 с остатком и быстро стирает. "Странно... - думает он, ероша волосы и краснея. - Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая"... Учитель глядит в ответы и видит 75 и 63. "Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то". - Решайте же! - говорит он Пете. - Ну, чего думаешь? Задача-то ведь пустяковая! - говорит Удодов Пете. Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич. Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет. - Эта задача, собственно говоря, алгебраическая, - говорит он. - Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил... понимаете? Теперь, вот, надо вычесть... понимаете? Или, вот что... Решите мне эту задачу сами к завтраму... Подумайте... Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол. - И без алгебры решить можно, - говорит Удодов, протягивая руку к счетам и вздыхая. - Вот, извольте видеть... Он щелкает на счетах, и у него получается 75 и 63, что и нужно было. - Вот-с... по-нашему, по-неученому.

Суть в том, чтобы найти ответ только с помощью арифметики, то есть использовать неизвестные нельзя. Об этой задаче рассказал коллега по работе.
Ответ
Если бы купец купил 138 аршин только синего сукна, тогда он потратил бы 138*5=690 рублей. Но он потратил 540 рублей. Разница 690-540=150 рублей возникает из-за того, что черное сукно стоит на 5-3=2 рубля дешевле. Поэтому можно вычислить купленное количество черного сукна разделив 150 на 2. Получим, что купец купил 75 аршин черного сукна. Тогда за синее сукно он заплатил 540-75*3=315 рублей. Отсюда получаем 315/5=63 аршина синего сукна. Как видите, задачу можно решить применяя только арифметические операции.

В каком месте построить мост?

Несложная задачка от моего знакомого. Есть два дома: А и B. Между ними протекает река, через которую нужно построить мост. Мост, естественно, должен быть перпендикулярен берегам реки. Расстояния от домов до ближайших к ним берегов разное. Требуется выбрать для моста такое место, чтобы путь от дома А к дому B был минимальным.
Ответ
Так как ширина реки постоянна (обозначим её s), то при выборе пути это значение можно не учитывать. То есть можно предположить, что реки нет, а все точки на правом берегу сдвинуть на расстояние s к левому берегу. Точка B перейдет в точку C. Теперь нужно искать кратчайшее расстояние между точками A и C. Это, естественно, будет отрезок AC. Отрезок АС пересекает левый берег реки в точке D. В этом месте и нужно строить мост. Так как DC равно BE, то путь ADEB будет минимальным.

Контакты

Предложения о сотрудничестве, а также пожелания относительно работы сайта вы можете оставлять в виде комментария к этому сообщению или присылать на почтовый адрес:

О сайте

Этот блог представляет из себя сборник различных задач и головоломок, которые по тем или иным причинам показались мне интересными. Если вы любите в свободное время поломать голову над решением какой-нибудь задачки, то сможете найти на этом сайте что-нибудь интересное именно вам.

*