Яранга и метро

Вопрос одной из игр ЧГК 1986 года. Знатоки ответили досрочно.

С детской задачей на смекалку про кубики пока никто не справился.

Лингвистика

Занятная задача из области лингвистики.

Австралиец австрийского происхождения Чарльз К. Блисс (Charles K. Bliss, 1897–1985), вдохновившись примером китайских иероглифов, в 40-е годы XX века разработал систему знаков, которая, по его мнению, должна быть понятна всем людям независимо от их родного языка. Эта система получила название «блиссимволика».

Даны слова, записанные с помощью блиссимволики, и их переводы на русский язык в перепутанном порядке:

талия; деятельный; больной; губы; деятельность; дуть; западный; весёлый; плакать; слюна; дышать.

Задание 1. Установите правильные соответствия.

Задание 2. Укажите, что означают приведённые ниже картинки, если известно, что две из них имеют одно и то же значение:

Задание 3. Запишите с помощью блиссимволики:

(18) воздух; (19) туловище; (20) подниматься; (21) восток; (22) печальный.

Эту и другие интересные задачи можно найти на Элементах.

3x3x3

Каким образом куб размером 3x3x3 можно разделить на 21 кубик? При этом кубики не обязательно должны быть одинакового размера, но длина стороны каждого такого кубика должна быть целым числом.

16 лиц

Реклама одного телефона уверяет, что на этой картинке 16 лиц и телефон их может все найти. Попробуйте и вы это сделать. Картинку можно увеличить.

ОТВЕТ

Назовите профессию

"Речь его тиха, однообразна и монотонна. Между словами и между предложениями - очень веские паузы. Его редкие жесты - спокойны, ритмичны, медленны и обдуманно-осторожны, как, впрочем, и у всех первоклассных мастеров, которых сама профессия приучает навсегда быть поддельно-равнодушными и как бы притворно-сонными." Назовите профессию человека, для которого, по мнению Александра Куприна, резкие движения противопоказаны, опасны.

ВИДЕООТВЕТ

12 коней

Требуется расставить 12 коней на шахматной доске так, чтобы все незанятые поля были под боем. Если не считать "зеркального" варианта, то существует только одна такая расстановка.

update

Первым правильно ответил Эйч.
Ответ

Еще две головоломки с расстановкой фигур:
Три ферзя на поле 6x6.
8 фигур.

2 место

Восстановите результаты всех матчей в однокруговом футбольном турнире, в котором участвовало 4 команды, если известно, что "чистое" второе место заняла команда, набравшая 3 очка. "Чистое" место означает, что больше нет команд набравших столько же очков. За выигрыш дается 3 очка, за ничью - 1 очко и за поражение - 0 очков.

update

Первым правильно ответил ERUDIT.
Ответ

Ещё две головоломки про футбольные турниры:
ЧМ-1986.
Ошибка в таблице.

1000 бутылок

Имеются 1000 бутылок с вином. В одной из них вино испорчено. Имеются 10 белых мышей, с помощью которых нужно обнаружить плохое вино. Если мышь выпьет плохого вина, ровно через 10 минут она приобретает яркую фиолетовую окраску. Разрешается накапать вина из разных бутылок каждой мыши и дать им выпить одновременно, а потом ждать. Придумайте способ, позволяющий через 10 минут и 1 секунду определить бутылку с испорченным вином.

update

Первым правильно ответил Yurko.
Ответ

Пронумеруем все бутылки от 1 до 1000 и напишем на каждой ее номер в двоичной системе счисления; для номеров, меньших 512, допишем слева нули так, чтобы всего на каждой бутылке были написаны десять цифр. Также присвоим каждой мыши номер от 1 до 10 и дадим k-й мыши смесь вина из тех бутылок, на которых k-я цифра - единица. Когда пройдут десять минут, выпишем десять цифр - единицу на k-м месте, если k-я мышь изменила цвет, иначе - ноль. Полученная двоичная запись будет номером испорченной бутылки.

Пока правильных ответов на задачу про шесть гирь не было, попробуйте.

Сумма

Даны пятьдесят различных натуральных чисел, двадцать пять из которых не превосходят 50, а остальные больше 50, но не превосходят 100. При этом никакие два из них не различаются ровно на 50. Найдите сумму этих чисел.

Так удастся ли провести прямую, которая будет пересекать не менее 4 окружностей?

update

Первым правильно ответил Yurko.
Ответ

Вычтем 50 из каждого числа, которое больше 50. По условию ни одна из разностей не равна ни одному из 25 чисел, которые не превосходят 50. Поэтому вместе с ними разности дают 50 различных натуральных чисел, которые не превосходят 50, то есть это все числа от 1 до 50. Их сумма равна 51*25, а сумма всех исходных чисел равна 51*25+50*25=2525.

Неправильные надписи

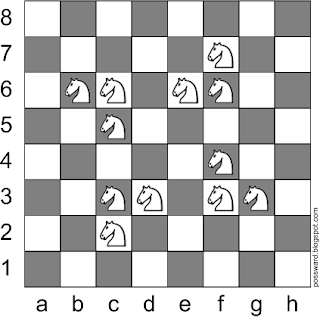
Имеется шесть гирь, массы которых 1 г, 2 г, 3 г, 4 г, 5 г и 6 г. На каждой гире надписана ее масса, но надписи возможно перепутаны. Как за два взвешивания на чашечных весах выяснить, есть ли среди надписей неправильные (не важно, какие именно)?

update

В напряженной борьбе победил Yurko.
Ответ

Первое взвешивание: 1+2+3=6. Гиря под номером 6 должна быть самой тяжелой. Гири с надписями 1, 2 и 3 вместе тоже должны весить 6 г, в противном случае их общий вес будет больше. Если весы в равновесии, значит на гире 6 надпись нанесена правильная. Надписи на гирях 1, 2 и 3 могут быть перепутаны, но только между собой, а не с гирями 4 и 5. Если весы не уравновешены, то сейчас на весах есть гири 4 г и/или 5 г, и неправильность нанесения надписей уже определена.
Второе взвешивание. Теперь у нас есть "эталон" - гиря весом 6 г. Кроме того, надписи могут быть перепутаны только внутри наборов гирь 1, 2, 3 и 4, 5. Тогда на весах можно сравнить по гире с каждого набора с эталонной. Например, на одну чашу положить гири из наборов с максимальным весом 5+3=8, а на другую - эталон и гирю с минимальным весом 1. Тогда во втором взвешивании получим 5+3>6+1. Причем чаша с гирями 5+3 перевесит только в том случае если надписи на гирях 5 и 3 правильные. Тогда можно сделать вывод, что надписи остальных гирях тоже правильные. В противном случае получим равновесие (перепутаны 1 и 2), или перевесит чаша 6+1 (уменшьшится вес 5+3 и увеличится 6+1).

1*******7

В последовательности звездочками обозначены числа. Сумма любых трех соседних чисел в этой последовательности равна 15. Найдите второй член последовательности, то есть число, обозначенное первой звездочкой.

update

Быстрее всех был Grom в твиттере.
Ответ

7.

Поскольку сумма трех последних чисел равна 15, а последнее число равно 7, то сумма шестой и седьмой звездочек равна 8, поэтому пятая звезда равна 7 (ведь сумма пятой, шестой и седьмой звездочек также равна 15). Дальше рассуждаем аналогично и получаем, что вторая звездочка равна 7. Сумма же первых трех чисел также равна 15, поэтому на месте первой искомой звездочки должна стоять 7.

Иван Васильевич меняет профессию

Пробуем найти очередной киноляп. На этот раз в эпизоде всем известного фильма "Иван Васильевич меняет профессию".

update

Быстрее всех был auti.
Ответ
Со стола пропал кинжал.

21 г

Среди 11 внешне одинаковых монет 10 настоящих, весящих по 20 г, и одна фальшивая, весящая 21 г. Имеются чашечные весы, которые оказываются в равновесии, если груз на правой их чашке ровно вдвое тяжелее, чем на левой. Как за три взвешивания на этих весах найти фальшивую монету?
Как найти 4 фальшивые монеты?

update

Первым правильно ответил Медалист.
Ответ
Подробный ответ в комментариях.

AC=2AB

Дан отрезок AB. С помощью одного только циркуля найдите точку C, такую, что отрезок AC=2AB.

Про отрезок нужной длины.
Про угол нужной величины.
Про центр окружности.

update

Первым правильно ответил Эйч.
Ответ

Вначале проводим окружности с центрами в точках А и В и радиусом АВ. Пусть D - одна из точек пересечения этих окружностей. Далее тем же раствором циркуля на окружности с центром В откладываем дуги DE и EC. Точка С - искомая точка.

Задача Набокова

Оказывается, что писатель Владимир Набоков был видным шахматным композитором. Вот одна из его самых известных задач. Белые делают мат в три хода.

update

Первым правильно ответил Waleriy.
Ответ
1. h3, h4.
2. Лh7, hg.
3. h4X

1. h3, Крh6.
2. h4, g5.
3. hgX

1. h3, Крh4.
2. Л:g6, gh.
3. Сf6X