
Игрок бросает десятирублёвую монету на стол, на поверхности которого нарисована сетка с ячейками в виде квадратов. Диаметр монеты 22 мм, длина стороны квадратной ячейки 40 мм. Если монета попадает внутрь любого квадрата, то игрок выигрывает, в противном случае он теряет свою монету. Считаем, что монета всегда падает на стол и вероятность падения монеты в любую точку стола одинакова, толщиной линий сетки пренебрегаем. Каковы шансы выиграть в этой игре?
Ответ
Головоломка Колумба.
update
Первым правильно ответил dbsergey.Ответ
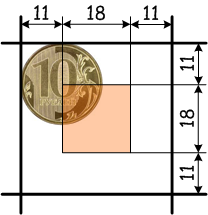
Игрок выигрывает в том случае, если центр монеты попадает в квадратную зону, которая отмечена оранжевым цветом. Следовательно, вероятность выигрыша будет равна отношению площадей маленького и большого квадратов: P=(18^2)/(40^2)=324/1600=0,2025

Головоломка Колумба.
1. Считаем координаты центра монеты случайной величиной.
ОтветитьУдалить2. Вероятность выигрыша равна отношению площади фигуры, внутрь которой должна упасть монета для победы игрока, ко всей площади.
3. Фигура из пункта 2 - это совокупность четырех квадратов, каждый из которых расположен внутри каждого из квадратов исходной фигуры.
4. Сторона каждого из квадратов пункта 3 равна 40-11-11=18. Площадь - 324. Площадь всех четырех - 1296.
5. Площадь исходной фигуры равна 6400. Вероятность победы - 0.2025.
Верно! Можно было рассмотреть только один квадрат.
Удалить